Long passwords are good, actually

Why Your Passwords are Probably Not Safe: An Oversimplified Explanation

By Gabriel Thompson January 17, 2022 (OLD POST)

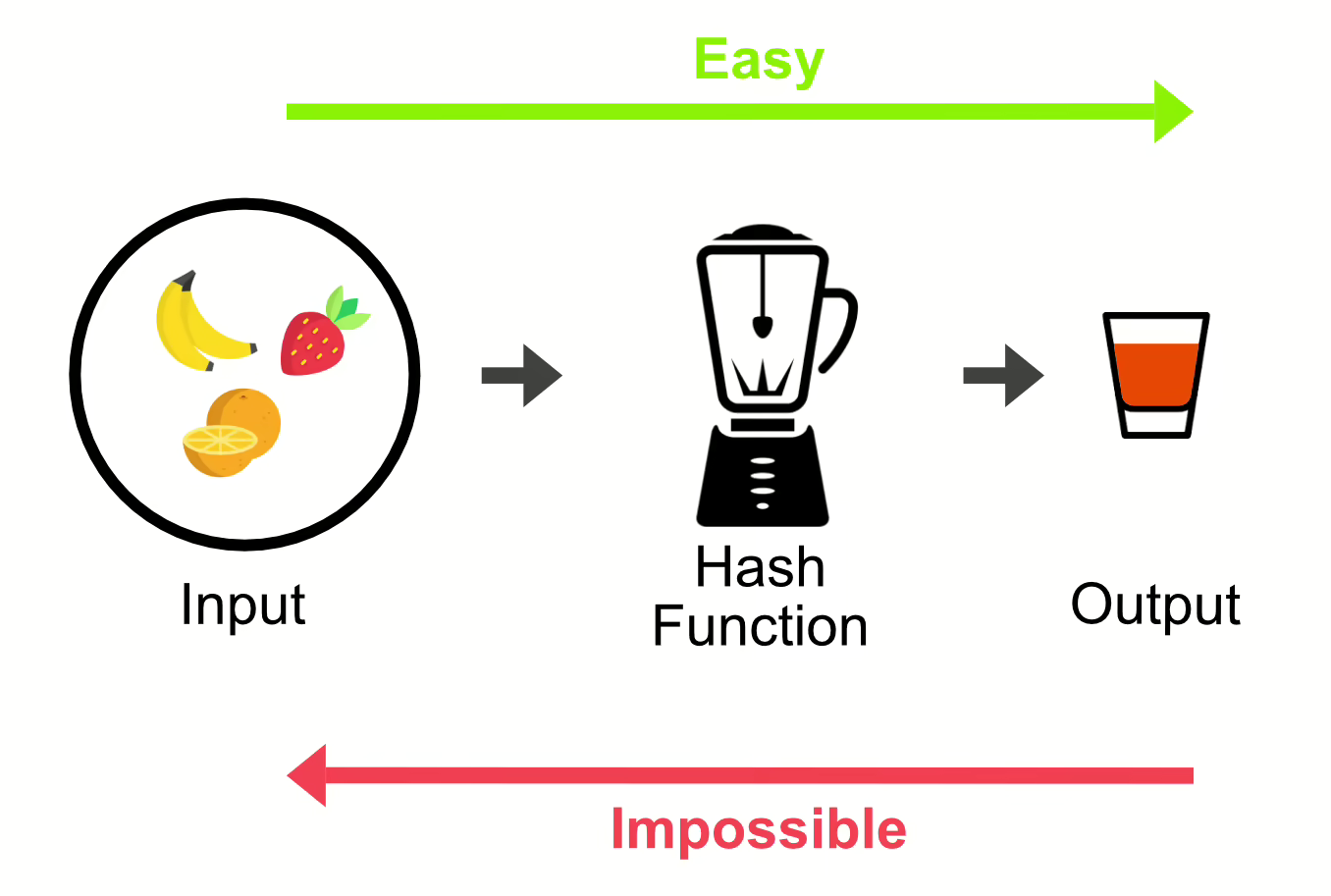
Image credit: https://www.techsolvency.com/passwords/dehashing-reversing-decrypting/

It would be a massive understatement to call authentication important to computing. With computers storing everything from medical records, to social media posts, to private emails, knowing who is trying to access a piece of data is crucial to any system that stores data. Data leaks, often caused by computers misidentifying who was trying to access a piece of data, can have consequences ranging from minor embarrassments to financial disasters.

Because of how important authentication is, computer scientists, companies, and governments have put a lot of effort into creating methods to ensure that only the intended people can access a piece of data.

Basic passwords

There are many different methods of authentication. Lately, there have been new(er) inventions such as two-factor authentication, or fingerprint authentication. However, the most common (and oldest) of these methods is a password system. The idea behind a password is simple: store the username and corresponding password of each account in a file. Then, when someone logs into the system, prompt them for their username and password. If this password they entered matches the appropriate password listed in the file, allow them in. Otherwise, do not allow them in.

The data storing the usernames and passwords would look something like this:

When a user logs in, all the system has to do is compare the password the entered with the password listed under the username they entered in. For example, if the user entered gabriel for the username and password123 for the password, they would be let in to the gabriel account. However, if they instead entered gabriel for the username and password124 for the password, they would not be let in, as password124 does not match password123, the password entry that corresponds to the username gabriel.

This system, on its face, seems to work almost perfectly. By guessing random passwords, it would millions, or even billions of guesses to get most passwords. Even if only 64 characters were allowed in passwords (uppercase and lowercase letters, numbers, and underscore and dash), there would already be \(64^5\) (roughly 1 billion) possible passwords of length 5. Because entering an account without knowing its password would require guessing random passwords, it could take up to 1 billion guesses to enter an account with a password length of just 5. And besides, most systems don't allow you to make more than 5 passwords attempts, let alone 1 billion.

However, this method has a critical flaw. Gaining access to the file storing the passwords would give you access to not only users' personal information -- but also their passwords, which they more than likely also use for other websites and services.

Although it may seem unlikely for someone to gain access to the password file, it is never good to have a single point of failure, especially one as devastating as this. It is because of these flaws that almost no reliable websites use a database that directly lists each person's username and password.

SHA-256

So, you might wonder: if websites don't use the above method, how do they store people's passwords? Well, the answer involves an algorithm called SHA-256.

SHA-256 (sort of) stands for "Secure Hash Algorithm - 256 bits". SHA-256 is an algorithm that takes in an input of any size, and outputs a random-ish 256-bit sequence. For example, converting "gabriel" to SHA-256 yields the following result (when converted to hexadecimal):

gabriel -> ff06535ac1029cca2fc2b86ac7355a7b4e0b8d839fc76b51d30833f4e1347ddc

In the above example, "gabriel" is being converted to its binary equivalent, and is then being passed through the SHA-256 function. The result (also known as the hash of "gabriel") is displayed in hexadecimal form. This result isn't super remarkable -- it is, on its face, just a series of 64 random hexadecimal digits. But, notice what happens if I change one character in "gabriel", and run this through SHA-256:

gabriek -> 88446045edff58c90f02556f590841c2145dbcdffe7778808edbf183cbb5a511

We get a completely different result! What makes SHA-256 so amazing is the fact that there is no² algorithm to reverse this conversion. There is absolutely no correlation between the input to SHA-256, and its output, and so in order to reliably reverse a SHA-256 hash, you literally need to go through every random series of characters, and convert each to SHA-256 to see if the result matches the hash you are trying to reverse. This would take an unfathomably long time. For example, I can give you this output hash:

43bc993ff0f1d2c27c225568d39844db863bb0dcb0299815defa8b3dd43521e1

I generated this by bashing on the home row keys, and it would take literally billions of years on a supercomputer (if not more) to find out exactly what I bashed on my keyboard to generate this output.

Because SHA-256 is effectively irreversible, we can say that SHA-256 is a one-way function.¹

How SHA-256 applies to authentication

But, what does SHA-256 have to do with passwords and authentication? To answer this, let's revisit our password sheet that an imaginary website could use to store user login information.

This system worked by comparing the password a user enters when logging in, to the password written in the table. The problem with our system was that all of the passwords were written directly in the file. However, what if we instead converted all of the passwords to SHA-256, and stored only the hashed versions of the passwords, rather than the original passwords?

Our new password file would be the following:

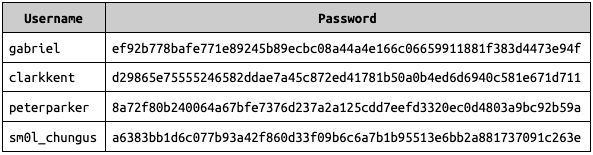
Here, ef92b778bafe771e89245b89ecbc08a44a4e166c06659911881f383d4473e94f is just password123 when passed through SHA-256, and all of the other passwords are just the SHA-256 version of their original values. Now, if a user types in a password, rather than comparing it to the stored password, we can convert the password the user entered through SHA-256, and then compare the resulting hash with the stored hash!

Take, for example, the account peterparker, and imagine that the user enters the correct password (justletmein). This entered password will be converted to SHA-256; the output of this will be

8a72f80b240064a67bfe7376d237a2a125cdd7eefd3320ec0d4803a9bc92b59a

The program can then check to see if that matches the password listed in the passwords file. Because it does match, the program knows the user entered the correct password. However, imagine that the user entered the wrong password, e.g. justletmein?, which has a question mark at the end. When this password is converted to SHA-256, the output will be

01c308dea0e294b70123dbf9cf041e927f4bf83279d1b6569f85bcc793f53a05

The program will then check if this matches with the resulting hash listed in the password file, which it does not. The program therefore knows that the user entered the wrong password, and will not be let in.

Through this system, our program is able to successfully authenticate a user without ever storing their actual password. Because of these benefits, just about every secure website uses some form of hashing for storing user passwords.

Storing only hashed versions of passwords causes some pretty interesting effects. For example, every website that hashes your password (which is hopefully all of them) doesn't actually know what your password is. It's bizarre, but Google does not actually know your password. This is part of the reason that password recovery is such a difficult process.

Another interesting effect of using hashing is that there are actually multiple possible passwords that you can type in, which will log you into an account. Because SHA-256 takes in an input of any size, there are infinite possible distinct inputs to the function. However, because the output is always 256 bits, there are only \(2^{256}\) possible distinct outputs. Because an infinite group of distinct inputs is mapping to a finite group of distinct outputs, there must be multiple distinct inputs that map to the same output. And, because \(\infty\) is significantly larger than \(2^{256}\), we can say almost certainly, that there are infinite possible inputs that map to each output hash. Therefore, there are infinite other possible passwords which you can type in which will log you into your account. However, because only \(\frac{1}{2^{256}}\) of all passwords will convert to the correct hash, it is extremely unlikely that anyone will ever discover any of the other valid passwords into your account. If anyone did, it could be said that SHA-256 is "broken". However, that is very unlikely to happen soon.

Why you still probably need a strong password

Given that SHA-256 is irreversible, it's easy to think that it is completely impossible for anyone to find your password if they're hashed. However, this is only really true if your passwords are strong.

For example, imagine your password is abc123, so its resulting hash is:

6ca13d52ca70c883e0f0bb101e425a89e8624de51db2d2392593af6a84118090

If a hacker were to gain access to the passwords file, they will not be able to directly reverse your hash. However, they might have built up a dictionary of common passwords, and they're corresponding hashes. Because abc123 is a common password, if they notice that you have its corresponding hash, they can quickly determine that your password is abc123. So, although SHA-256 may not be easily reversible, it is certainly possible to find someone's unhashed password based on a hashed one.

abc123 is a very easy example, but many other passwords are simply a word followed by a number. This makes it very easy for a computer to go through every possible word followed by every possible 4 or 5-digit number, hashing each password and comparing it to the original hash to find the original password. Programs such as HashCat and John the Ripper have been created to "crack" hashes with incredible (and terrifying) efficiency, which they do by prioritizing searching through passwords that contain real words.

But don't fear! There are two ways which you can prevent against your password getting cracked:

Don't be famous. If you're not famous, it's less likely that a hacker will bother to put a costly amount of effort into cracking your password, because there's simply less on the line with your account. However, the much more sane and obvious solution is to...
Use a strong password. The only reason that hackers can revert people's hashes is because they use real words or expressions in their password. If your password is a random series of uppercase and lowercase letters and numbers, it becomes astronomically difficult to crack your password. A random 9-character password with 64 character choices could take up to \(64^9\), or roughly 18 quadrillion hash attempts. Worried that's not enough security? Add one more character, and your password becomes 64x harder to crack.

At the log-in page, a hacker may only be able to attempt to log into your account five or so times before getting locked out. But if (when?) a service you use experiences a data breach, hackers can have millions, or even billions of attempts at your password. So yes, having a strong password actually is helpful.

¹ If you're interested in how the SHA-256 algorithm actually works, you can learn more about it here. I did not go over it in this post because it's dense, and a bit of a tangent.

² *polynomial-time

Gabriel Thompson's Personal Blog

Recent posts Archive